Tissue growth model and its numerical simulation
Proposed a viscoelastic growth model and simulate it using FEM and PINNs
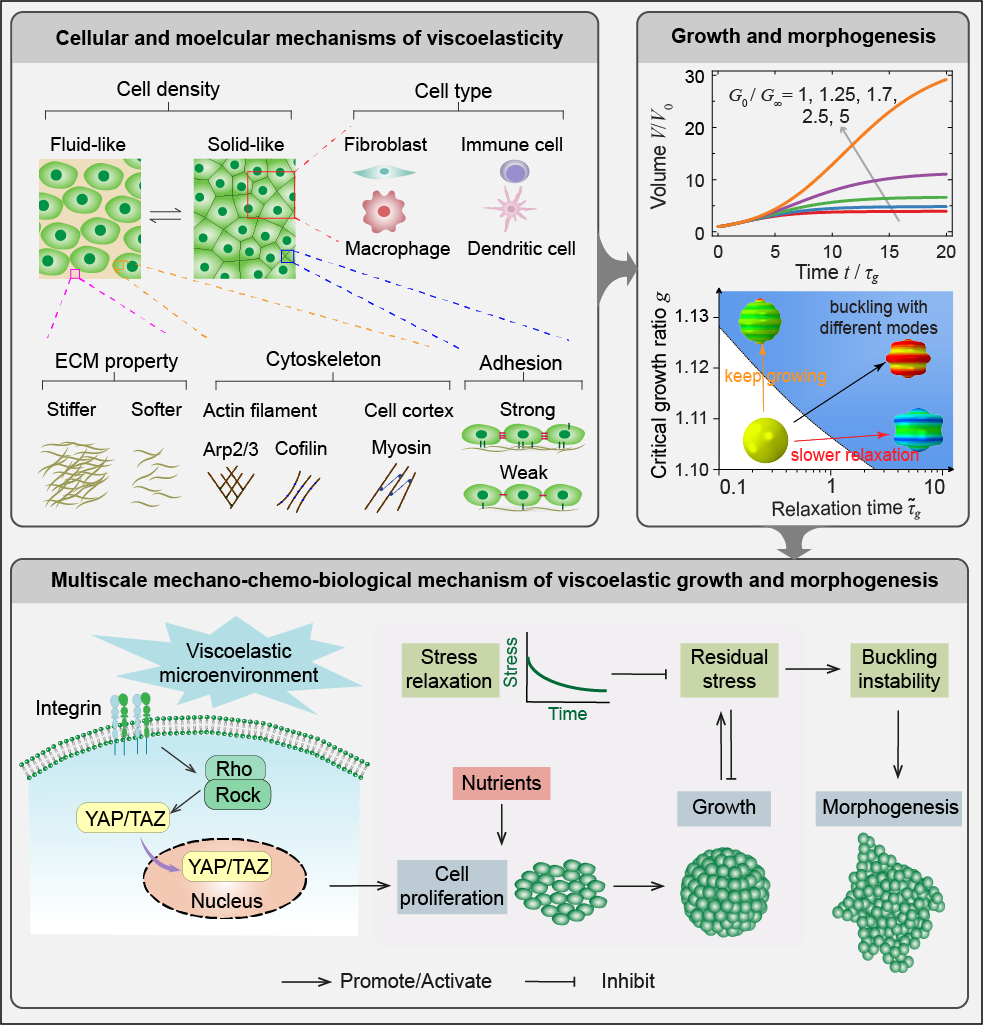
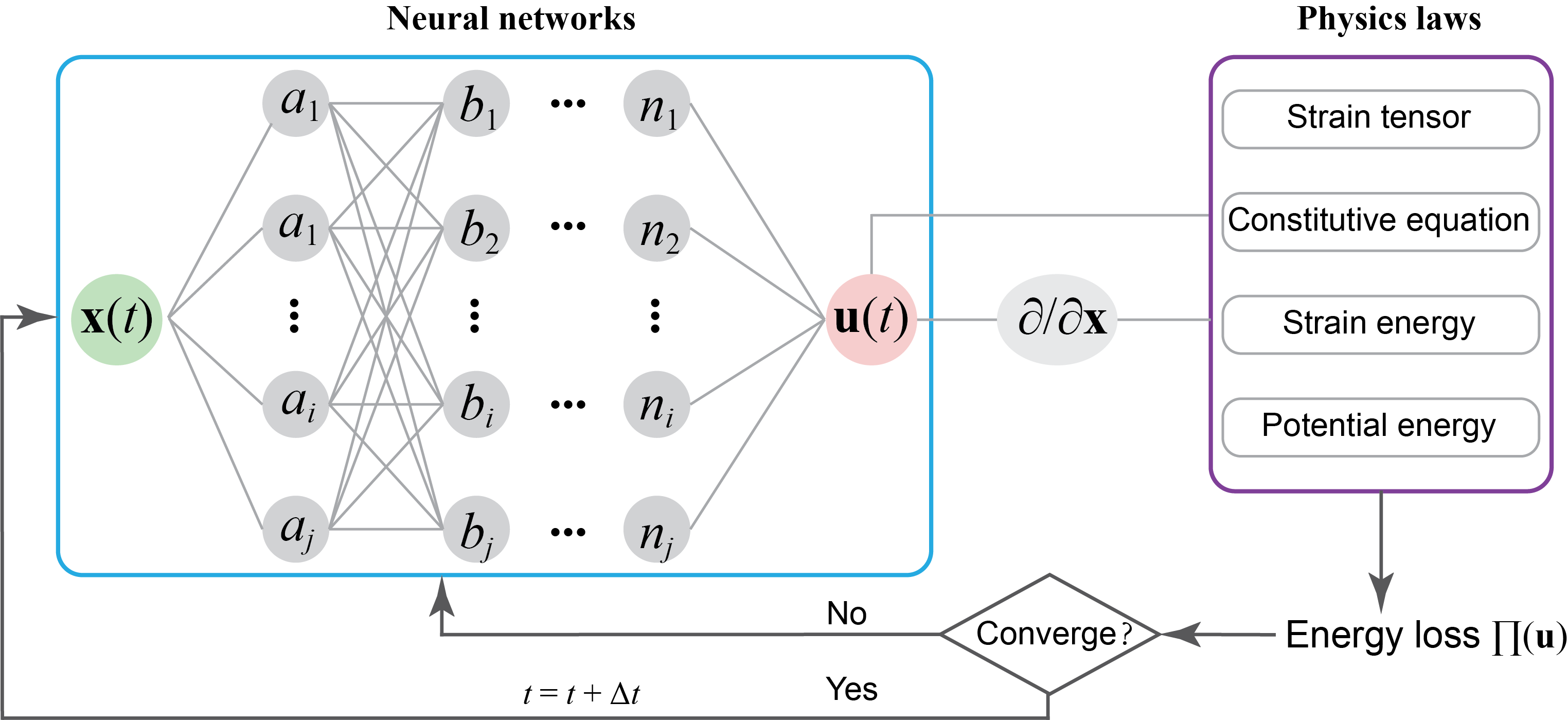
Most soft biological tissues feature distinct mechanical properties of viscoelasticity, which play a significant role in their growth, development, and morphogenesis (Figure 1a). To reveal the biophysical mechanisms, we first proposed a mechanobiological viscoelastic model in the framework of thermodynamics (Lin et al., 2025). Then, we used a more novel method, the physics-informed neural network (PINN) to simulate the tissue growth and morphological evolution (Lin et al., 2026), (Figure 2, and the open-source code in Github). With PINN, buckling occurs naturally under the critical states during the oscillated training process without introducing artificial perturbations. Our studies have demonstrated that viscoelasticity facilitates sustained tissue growth and significantly influences the critical conditions of surface wrinkling and tissue morphology. In the future, we hope to apply the cross-scale theories, e.g., the strain gradient viscoelasticity (Lin & Wei, 2020), to characterize the multiscale / crossscale properties of biological tissues.